//-->

Alan ve hacim bağıntıları

ÇEMBER VE DAİRE NE DEMEKTİR?

Çemberin içi boş halka gibidir. (yüzük,simit)
Dairenin içi dolu taralıdır. (madeni para,gazoz kapağı)

ÇEMBERDE AÇILAR:
Merkez açı: Köşesi merkez üzerinde olan açıya merkez açı denir.Merkez açı gördüğü yayın ölçüsüne eşittir.

Çember açı (çevre açı): Köşesi çember üzerinde olan açıya çember açı yada çevre açı denir.Çevre açı gördüğü yayın yarısına eşittir.

Aynı yayı gören çevre açının ölçüsü, merkez açının ölçüsünün yarısıdır.

Aynı yayı gören çevre açıların ölçüleri eşittir.

Çemberde çapı gören çevre açıları 90 derecedir.

ÇEMBERDE YAYLAR:

Majör çember yayı: Merkez açının kenarlarının çemberi veya daireyi kestiği noktaların arasındaki yaylardan büyük olana majör (büyük) çember yayı denir.

Minör çember yayı: Merkez açının kenarlarının çemberi veya daireyi kestiği noktaların arasındaki yaylardan küçük olana minör (küçük) çember yayı denir.Merkez açının gördüğü yay minör yaydır.

ÇEMBER’İN VE DAİRE’NİN ÇEVRESİ:
Ç = 2.π.r
(π=3,14 alırız r daire veya çemberin yarıçapı)

örnek: Yarıçapı 5cm olan çemberin çevresini bulunuz.
Ç = 2.π.r
Ç = 2.3.5 = 30cm (π=3 aldık)

DAİRE’NİN ALANI:
A = π.r.r
(π=3,14 alırız r dairenin yarıçapı)

örnek: Yarıçapı 4cm olan dairenin alanını bulunuz.
A = π.r.r
A = 3.4.4 = 48cm2(cmkare)

DAİRE DİLİMİNİN ALANI:
A = π.r.r.x / 360º
(π=3,14 alırız r dairenin yarıçapı, x açısı daire diliminin arasında kalan merkez açı)

örnek: Merkezde oluşan 60º lik açının taradığı ve yarıçapı 10cm olan daire diliminin alanını bulunuz.
A = π.r.r.x / 360º
A = 3.10.10.60º / 360º
A = 300 / 6 = 50cm2

ÇEMBER YAYININ UZUNLUĞU:
Ç = 2.π.r.x / 360º
(π=3,14 alırız r çemberin yarıçapı, x açısı çember parçasının arasında kalan merkez açı)

örnek: Merkezde oluşan 90º lik açının gördüğü ve yarıçapı 6cm olan çember yayının uzunluğunu bulunuz.
Ç = 2.π.r.x / 360º
Ç = 2.3.6.90º / 360º
Ç = 36 / 4 = 9cm

DİK DAİRESEL SİLİNDİR NEDİR?

Silindir geometrik bir cisimdir.

Hacmi: $V = pi cdot r^2 cdot h$

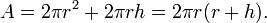
Yüzey alanı: $A = 2 pi r^2 + 2 pi r h = 2 pi r ( r + h ).,$

Bir dikdörtgenin bir kenarı etrâfında döndürülmesiyle elde edilir. Bu silindire dik veya eğik silindir denir. Alt ve üst tabanı dâiredir. Soba borusu dik silindire bir örnektir.

Matematikte silindirin genel tanımı şöyledir: Düzlemsel bir eğriyle bu eğrinin düzleminde bulunmayan bir doğru verildiğinde, dâimâ bu doğruya paralel kalmak şartıyla eğriye dayanarak hareket eden bir doğrunun taradığı yüzeye silindirik yüzey denir. Bu silindirik yüzeyle, bu yüzeyi kesen paralel iki düzlemin sınırladığı cisme silindir denir. Silindir yüzeyini meydana getiren doğrulardan herbirine ana doğru denir.

Silindire, taban eğrisine göre isim verilir. Eğri dâireye Şişe dâirevî silindir, elipse ise eliptik silindir denir. Silindirik yüzey için taban eğrisinin kapalı olması gerekmez. Parabolik silindir, hiperbolik silindir, birer silindirik yüzeydir. Dairevî silindirin ana doğrusu tabana dik değilse böyle silindire eğik silindir denir.

Taban yarıçapı “r”, yüksekliği “h” olan bir dik silindirin alan ve hacim formülleri şöyledir:

Yan alan: Y=2πrh

İki taban alanı: 2A=2πr2

Bütün alanı: S=Y+2A=2πrh+2πr2=2πr (h+r)

Hacmi: V= π r2. h

Bayındırlıkta: Bir şasiye monte edilmiş, tekerlek vazîfesi gören bir veya birkaç büyük mâdenî silindirden meydana gelen ve toprağı, şaseleri kaplayan malzemeyi sıkıştırmak ve ezmek için kullanılan, dökme demirden yapılmış büyük ağırlığa, şeklinden dolayı silindir adı verilir.

Otomobilde, tekstil ve kâğıt sanâyiinde çeşitli silindirler kullanılmaktadır.

SİLİNDİR’İN ALANI:
A = yanal alan + 2.taban alan
A = 2.π.r.h + 2.π.r.r
(π=3,14 alırız, r taban yarıçapı, h yükseklik)

örnek: Taban yarıçapı 1cm ve yüksekliği 4cm olan silindirin alanını bulunuz.(π=3)
A= 2.3.1.4+2.3.1.1= 24+6= 30cmkare

SİLİNDİR’İN HACMİ:
H = taban alan.yükseklik
H = π.r.r.h
(π=3,14 alırız, r taban yarıçapı, h yükseklik)
(konserve tenekesi)

örnek: Taban yarıçapı 4cm ve yüksekliği 5cm olan silindirin hacmini bulunuz.(π=3)
H= 3.4.4.5= 240cmküp

Silindirin Açınımı ve Açık Şekli